Black Holes and Cosmic Censorship

 

Introduction

Once a purely mathematical prediction from Einstein's theory of general relativity, black holes have been discovered to exist in nature. In the modern day, they have been used as the arena to broaden our understanding of gravity. In the past six years alone we have witnessed achievements such as the Nobel Prize for developments in black hole physics, the discovery of gravitational waves from two black holes colliding, and the first image of a black hole being taken. These advancements made for catchy headlines in the media, and along with movies like Interstellar that used black holes as a plot point, it is safe to assume the general public is aware that black holes exist. However, those interested in delving deeper into this subject -even those with a background in mathematics- may quickly become overwhelmed by the sheer amount of information.  This post will serve as an introduction to black holes and will only require basic knowledge in calculus. First, a bird's eye view of the machinery that is behind general relativity will be introduced, followed by a discussion on how black holes emerge out of theory. 

General Relativity: A Bird's Eye View

At the beginning of the 20th century, special relativity brought about discussions of the geometry of spacetime. Predictions such as length contraction and time dilation all originated from the fact that time and space were interconnected so that the cosmic speed limit stayed at the speed of light. However, the flat geometry that describes the spacetime in special relativity did not combine well with Newton's laws of gravity, therefore required a more fitting model. In 1912, Einstein had the idea that in the presence of matter, flat spacetime, as described by special relativity, will deform and have curvature. The geometric point of view went from a mathematical nicety to a description with a physical effect. When one talks about general relativity, the conversation often leads to differential geometry, manifolds, and other complicated mathematical objects. What the math intends to describe is a space that is not flat but has some notion of curvature. In this context, curvature can be described as any deviation from the expected Euclidean results, where one uses Pythagoras's theorem to measure distances and the shortest distance between any two points is a straight line.  

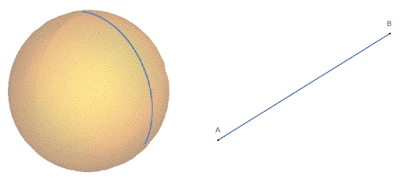
As an example, let's look at two 2d surfaces: a plane and a sphere. These two surfaces have different curvatures and, as a result, have different ways of measuring distance. To measure the shortest distance between two points on the plane, it is simply a straight line, as expected from the standard Euclidean result. However, on the surface of a sphere, the shortest distance between two points is a curved path.   This concept can be understood quite easily using a visual (Figure 1).

Figure 1.

Mathematically we have to develop a way to measure distances on all sorts of spaces, not just 2d surfaces. As a starting point, let's look at flat 3d space and how we measure distances between two points. s is defined here as the distance. Pythagoras's theorem gives us the shortest distance between two points, i.e a straight line. If we want to incorporate calculus and look at infinitesimal distances it is only a matter of using differentials (see Equation 1). 

Equation 1.

The differential form can be used for measuring distances for more general curves between two points, but still only in flat space. Notice the coefficient in front of each differential is one. Now as an exercise, let's use spherical coordinates instead of cartesian (see Equation 2).

Equation 2.

Nothing has happened to the space we are describing -it is still flat 3d space- but the coordinates we are using to label points in this space have changed, as have the coefficients in front of the differentials. Now, the coefficients depend on the coordinates themselves and are different for each differential. In this coordinate system, the coordinates have a different relationship to each other when measuring distances. The simplest example of this is the circle. For the same change in angle, one gets a larger arc length if the radius is larger. We can generalize the form of the equations in Equation 2 by putting a placeholder in front of the differentials while allowing differentials of different coordinates to be multiplied together (see Equation 3). 

Equation 3.

The Greek letters seen in the notation of Equation 3 are not to be interpreted as exponents; instead, they are indices that enumerate the different coordinates, and we sum over all the different coordinates. All the coefficients in front of the various differentials are the components of an object called the metric, labeled g with Greek letter indices. The metric is the crucial object that needs to be found if one is to determine the geometry of the space being considering. It should be noted that the metric for flat 3d space is different when one is using cartesian versus spherical coordinates, but it describes the same space. This places an important requirement for this new theory of gravity: it must be able to handle any coordinate transformation because the equations describe the same thing. The names give a hint. Equations in general relativity are true under general coordinate transformations, while equations in special relativity are only true under special coordinate transformations(i.e. Lorentz transformations). 

The metric for flat spacetime is similar to the flat space metric, except for the time coordinate, which has a negative sign (see Equation 4). The exact form comes from the theory, but the negative sign can be thought of as an indicator that time is inherently different from space given the fact that we can move freely in space but not in time. This metric has a special name, the Minkowski metric, and it is used in special relativity. Here c is the speed of light and remains constant. 

Equation 4.

The next step is to find the metric that describes spacetime that has matter present.  The metric must describe a space where the shortest paths are not straight lines, and it cannot be derived from the flat metrics via coordinate transformations.  To do this, Einstein used his postulate that matter creates curvature, and through many lines of math, one finds the now-famous field equations. 

Equation 5.

The equation in Equation 5 embodies the idea that matter brings curvature to spacetime. The left-hand side consists of derivatives of the metric with respect to all the coordinates, which have been grouped into objects known as the Ricci tensor and scalar. The right-hand side has a singular object called the energy-momentum tensor and tells us about the location of all the matter and energy in our space. Using this equation, the metric for various distributions of matter can be found.

Finally, the motion of objects in this spacetime can be found by minimizing the distance, s, between two points. These paths are called geodesics. This embodies the phenomenon that astronauts experience free fall in space- they don't feel any Newtonian force pushing them to Earth, rather they are following the shortest path in the curved spacetime.

Black Holes in General Relativity

Now that we know what the metric is, let us look at the first solution to the field equations, the Schwarzschild metric.  The coordinates used are the spherical coordinates we met earlier. It should be noted that this metric describes the curvature outside of the matter distribution -where a vacuum exists -and the matter is centered at r = 0. In addition, this metric also describes a matter distribution that is spherically symmetric and also static. The metric inside of the matter distribution is different and will not be discussed in this post. 

Equation 6.

The form of the metric in Equation 6 is more complex than the ones seen above but there are similarities. The coefficients in front of the angular differentials are the same as the ones for flat spacetime. These coefficients tell us that this matter distribution is spherically symmetric. The coefficients in front of the time and radius coordinate, however, have some interesting differences. Two radial coordinates produce infinities in the metric: r = 0 and r = r_s. The former is a single point, while the latter is a spherical surface of that radius. Identifying the divergences of functions is a standard practice in mathematics as it is helpful to understand their behavior. The spherical surface associated with r = r_s is called the event horizon, and its radius is called the Schwarzschild radius. This radius depends on the total mass M of the object producing curvature and some universal constant. However, this divergence in front of the radial differential is not real, it is simply a consequence of the coordinate system being used. If transformed into a different coordinate system, the divergence that existed would disappear. This surface does, however, describe a special place in space. All geodesics that start from this radius, even those for light, can never leave and go beyond this surface. In contrast, the divergence at r = 0 is distinct. No matter what coordinate transformation one does, this divergence remains. It is therefore called the singularity, in the mathematical sense of the word. 

Figure 2.

At this moment, we have a singularity that is covered by a surface from which no object, not even light, can escape. This can be visualized in Figure 2 where the black point in the center represents the singularity, and the spherical surface which surrounds it is the event horizon. This is what is known as a black hole. Black holes form when the radius of an object is equal to the Schwarzschild radius defined above. This formation happens when a star is not able to support itself and begins to undergo gravitational collapse. 

Another important thing to note is the size of the black hole depends on its mass, as seen from the Schwarzschild radius. These radii have a large range of values, which span from dozens of miles to several solar systems. 

So far, only non-rotating black holes static spacetime have been discussed. However, many stars in the universe rotate and have angular momentum, which is left to the black hole when the star collapses. This makes one wonder: what is the metric for a rotating black hole? Chronologically speaking, the solution for rotating black holes was found in 1963, nearly 50 years after the Schwarzschild metric was established. It's called the Kerr metric and its form is far more complicated.

Before the Kerr metric is introduced, the standard coordinate system that will be used should be explained. The coordinates used are those of an oblate spheroid, a three-dimensional ellipse. The transformation from the cartesian coordinates seen is in Equation 7 and  is given by:  

Equation 7.

Here, a is some constant that will be defined later, but if a = 0 then we recover our spherical coordinates. To gain some intuition for why these coordinates are used, first, let us consider why spherical coordinates are present in the Schwarzschild metric. The Schwarzschild metric describes the spacetime outside of spherically symmetric mass distributions.  This means that we can rotate our system about any axis and angle, and still be left with the same system, just like a sphere. Therefore, the most natural set of coordinates to choose are those which define spheres, i.e., the spherical coordinates as defined above. The same can be said about the oblate spheroid coordinates used in the Kerr metric. The Kerr metric describes the spacetime outside of rotating mass distributions, so the system is no longer spherically symmetric as there is now a preferred axis defined by the rotation axis. Consider how a sphere that rotates deforms. The sides start to bulge out due to the centrifugal force. Now consider plotting constant r surface using the oblate spheroid coordinates while increasing a. The resulting animation (Animation 1) depicts how we would expect the sphere to deform as it picked up more angular velocity. 

Animation 1.

Therefore, in the Kerr metric, it is no surprise that oblate spheroid coordinates are used as they are related to the deformation of spheres under rotation. In this case, rather than a solid sphere deforming, it is spherically symmetric spacetime itself deforming due to the rotation of the mass.

Now, it is time to introduce the Kerr metric. In Equation 8 and 9 below,  r_s is the Schwarzschild radius as defined above, J is the angular momentum of the mass distribution, and M is the mass.  

Equations 8 and 9.

As expected, the constant a, which made an appearance in our coordinate system, is related to the rotation of the mass distribution. While the form of this metric is far more complicated and its consequences are beyond our discussion, some visual differences between the Kerr metric and Schwarzschild metric can guide understanding. If a = 0, i.e. there is no rotation, we regain the Schwarzschild metric and spherical coordinates as expected. The most significant difference is that there is a non-zero coefficient in front of the cross-term of the time and phi differentials. This term in the metric not only makes the algebra significantly more laborious, but it has a substantial effect on the motion of objects in this spacetime.  Before we go hunting for infinities in our metric, let us look at some geodesics in Kerr spacetime.

To see how this cross-term affects the motion of objects, consider an object with mass starting at some radius with no angular momentum. If we first look at the Schwarzschild case, the motion of the object is what we would expect even using Newtonian gravity. The object falls radially inward towards the event horizon as seen in Animation 2.  All the orbital animations that are discussed here are equatorial (i.e., move only in the xy plane). Also, the dotted circles are the special surfaces (for the Kerr solutions; these will be discussed below). 

Animation 2.

If we add rotation to the black hole in the counterclockwise direction, the object will be dragged along in the same direction. Even though it had no orbital angular momentum, it gains velocity in the angular direction as depicted in Animation 3.

Animation 3.

Similarly, if we switch the rotation of the black hole to go clockwise, the object will be dragged along in that direction (see Animation 4). 

Animation 4.

This difference in the motion of objects is due to the cross-term in the metric. The fact that time and phi (i.e., the angular coordinate) are now related means that as time evolves the angular coordinate must also evolve, regardless of the initial motion of the object. This effect is known as frame-dragging, and it becomes stronger as the object gets closer to the black hole. To conceptualize this point, consider a black hole with clockwise rotation and an object now has an angular momentum in the opposite direction. The object begins on its initial trajectory but as it gets closer, it gets swept up in the rotation of the black hole and is forced to rotate with it (see Animation 5). Much like a boat going against the flow of a river, if the current gets too strong the boat will be forced to follow the river. 

Animation 5.

It should be noted that orbits where the object goes against the rotation of the black hole do exist, but these orbits occur much farther away from the black hole where frame-dragging has little effect. The Kerr metric has many more interesting features that arise from this cross-term, but let us move on to our game of looking for infinities in the metric. 

The first infinity we will investigate is when sigma goes to zero (see Equations 8 and 9).  Since the left-hand side is positive the only real solutions to this equation are the ones given.

Equation 10.

If we look at the coordinates using the solution as seen in Equation 10, we find that it defines a ring in the xy plane of radius a (see Equation 11). This is the same mathematical singularity that we identified as a point in the Schwarzschild metric; however, it is now a ring, and its radius increases with the angular momentum. This is an interesting result since classically a single point cannot have angular momentum; therefore, a shape such as a ring is intuitive as it can have angular momentum. So we have identifies our singularity (see Equation 11).  

Equation 11.

Our second divergence occurs when delta equals zero (see Equations 8 and 9). We obtain a quadratic equation that can be solved for and gives two solutions for an r value. These solutions are the event horizons (seen in blue and yellow in Figure 3), but now we have two of them. Their radii are larger than that of the ring singularity (seen in black in Figure 3) so these surfaces cover it completely.

Equation 12.

We can again plot these surfaces for some value of a. These horizons are no longer spheres but ellipsoids as they are deformed by the spinning of the singularity. 

Figure 3.

Once again, we are left with a singularity that is covered by event horizons from which nothing can escape. However, there is something unique about these results; it is possible to obtain a complex solution resulting in no event horizons. Looking at the r values for the event horizons from the quadratic formula, we obtain a complex number for r if a is large enough (see Equation 13). 

Equation 13.

By definition, r is a real number; therefore, for a values that are large enough, sigma will never be zero. Therefore, our black hole will lose its event horizons if it is spinning fast enough. This can be exemplified as seen in the animation below (see Animation 6).

Animation 6.

The two event horizons get closer and closer until they disappear completely -and we are left with what is known as a naked singularity. A singularity that is not covered by an event horizon is one that allows for light to escape it. This is quite a curious prediction considering we have never in nature observed a naked singularity. This inspired Roger Penrose's Cosmic Censorship Hypothesis which postulates that these naked singularities cannot exist in our universe. According to the hypothesis, the universe will always find a way to cover up, or censor, singularities so that we cannot see them. This hypothesis is still unproven as no one has been able to prove or disprove, the existence of naked singularities under the realistic gravitational collapse of stars. 

Conclusion

While general relativity is a rich subject that has been studied and tested for over a hundred years, this post aimed to provide a macroscopic view of the subject from which one can draw intuitive understanding. Hopefully, it has give a tangible perception of the essence of black holes, and sparked interest in those who are either starting their journey into the subject, or others who are simply curious to know more.

(This post was made for the 3Blue1Brown Summer of Math Exposition)